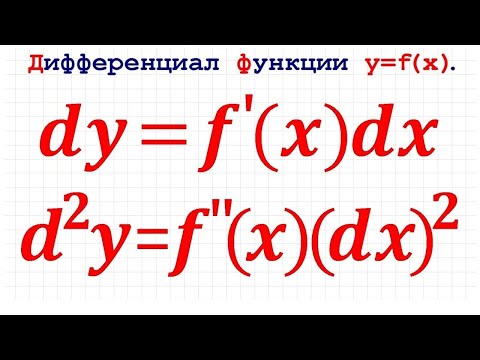
Часткові похідні в обчисленні - це похідні багатоваріантних функцій, прийнятих відносно лише однієї змінної функції, трактуючи інші змінні як би константи. Повторні похідні функції f (x, y) можуть прийматися відносно однієї і тієї ж змінної, даючи похідні Fxx і Fxxx, або приймаючи похідну відносно іншої змінної, отримуючи похідні Fxy, Fxyx, Fxyy тощо. Частково похідні, як правило, не залежать від порядку диференціації, тобто Fxy = Fyx.
Обчисліть похідну функції f (x, y) по відношенню до x, визначивши d / dx (f (x, y)), трактуючи y так, ніби це константа. Використовуйте правило продукту та / або правило ланцюга, якщо це необхідно. Наприклад, перша часткова похідна Fx функції f (x, y) = 3x ^ 2 * y - 2xy є 6xy - 2y.
Обчисліть похідну функції по відношенню до y, визначивши d / dy (Fx), трактуючи х як би константу. У наведеному вище прикладі часткова похідна Fxy 6xy - 2y дорівнює 6x - 2.
Перевірте правильність часткової похідної Fxy, обчисливши її еквівалент Fyx, взявши похідні у зворотному порядку (спочатку d / dy, потім d / dx). У наведеному вище прикладі похідна d / dy функції f (x, y) = 3x ^ 2 * y - 2xy дорівнює 3x ^ 2 - 2x. Похідна d / dx 3x ^ 2 - 2x дорівнює 6x - 2, тому часткова похідна Fyx ідентична частковій похідній Fxy.