
Зміст
Для того, щоб дві форми були конгруентними, кожна повинна мати однакову кількість сторін і їх кути також повинні бути однаковими. Найпростіший спосіб визначити, чи поєднуються дві фігури, - це обертати одну з фігур, поки вона не вишикується іншою, або просто скласти фігури один на одного, щоб побачити, чи стирчать якісь кінці. Якщо ви не в змозі перемістити фігури фізично, ви можете використовувати формули, щоб визначити, чи фігури є конгруентними.
Конгруентні кола
••• Ray Robert Green / Media DemandУсі кола мають однаковий кут у 360 градусів. Єдиним фактором, що визначає збіжність двох кіл, є порівняння їх розмірів. Діаметр - це пряма лінія, що проходить через центр кола від краю до краю, тоді як радіус кола - довжина від його центру до його зовнішнього краю. Вимірювання будь-якого з цих обох кіл докаже, чи вони є конгруентними.
Паралелограми
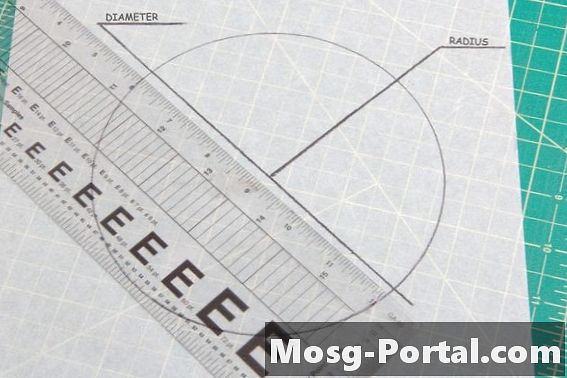
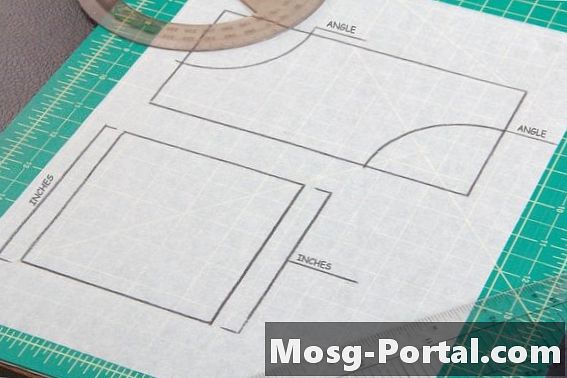
Паралелограм має дві пари паралельних сторін, таких як квадрати і прямокутники. Протилежні сторони або кути паралелограма мають однакову міру, тому необхідно зробити два кутові або бічні вимірювання на паралелограмі, по одному з кожної пари сторін, щоб порівняти конгруентність з іншою формою.
Трикутники
••• Ray Robert Green / Media DemandДля того щоб знайти збіжність трикутників, потрібно визначити розмір кожного кута або сторони, оскільки всі три можуть бути різними. Існує три постулати, які можна використовувати для ідентифікації конгруентних трикутників. Постулат SSS - це коли ви вимірюєте всі три сторони до кожного трикутника. Постулат ASA говорить, якщо якісь два кути та їх сполучна сторона збігаються з іншими трикутниками, то вони є конгруентними. Постулат SAS робить зворотне, вимірюючи дві сторони та їх кут з'єднання для порівняння з іншим трикутником.
Теореми конгруентних трикутників

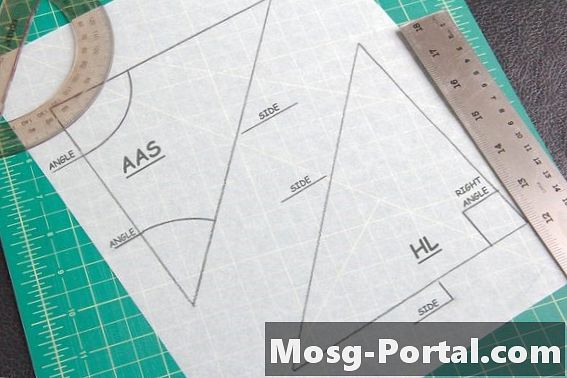
Дві теореми корисні для знаходження конгруентних трикутників. Теорема ААС говорить, що якщо два кути та сторона, що не з'єднує два, дорівнюють іншій трикутнику, то вони є конгруентними. Теорема Гіпотенуза-Нога стосується лише трикутників з одним 90-градусним або «правим» кутом. Це коли ви вимірюєте гіпотенузу - сторону, протилежну куту 90 градусів, - і одну з інших сторін трикутника, щоб порівняти з іншою формою.