Зміст
У геометрії шестикутник - це багатокутник із шістьма сторонами. Звичайний шестикутник має шість рівних сторін і рівні кути. Звичайний шестикутник загальновизнаний із соти та внутрішніх приміщень Давидової зірки. Шестигранник - це шестигранний багатогранник. Звичайний шестигранник має шість трикутників з ребрами однакової довжини. Іншими словами, це куб.
Формула площі шестикутника
Формула площі правильного шестикутника зі сторонами довжини "а" дорівнює 3 --- sqrt (3) --- a ^ 2/2, де "sqrt" позначає квадратний корінь.
Виведення
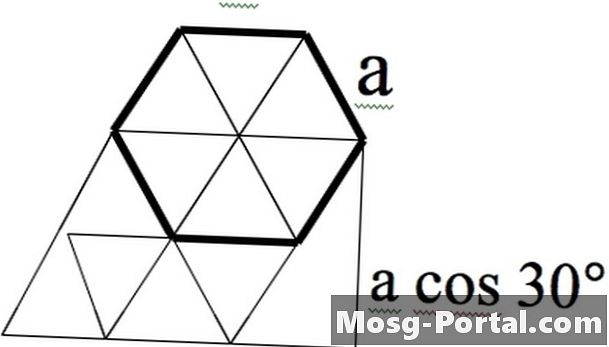
Правильний шестикутник можна розглядати як шість рівносторонніх трикутників сторін a. Їх кути - 60 градусів, тому кути в шестикутнику - 120 градусів. Трикутники можуть бути розширені нижче шестикутника, щоб утворився паралелограм сторін 2а. Для визначення висоти цього паралелограма можна створити більший трикутник, який дорівнює 2a --- cos 30 ° = a --- sqrt (3).
Отже, паралелограм на рисунку має висоту площі --- основа = (a --- sqrt (3)) --- 2a = 2 --- sqrt (3) --- a ^ 2.
Але це для паралелограма, який складається з 8 рівносторонніх трикутників. Шестикутник складався лише з 6. Отже, площа шестикутників становить 0,75 від цього, або 3 --- sqrt (3) --- a ^ 2/2.
Чергове походження
Шість рівносторонніх трикутників у шестикутнику мають сторони "а". Їх висоти, h, є, за теоремою Піфагора, sqrt = a --- sqrt (3) / 2.
Отже, площа трикутника дорівнює (½) --- основа --- висота = (а) ---. Шість трикутників у шестикутнику дають площу 3 --- sqrt (3) --- a ^ 2/2.
Об'ємна формула шестигранника
Формула об’єму правильного шестигранника сторін "а" дорівнює ^ 3, оскільки звичайний шестигранник - куб.
Площа поверхні - це, звичайно, ^ 2 --- 6 сторін = 6a ^ 2.