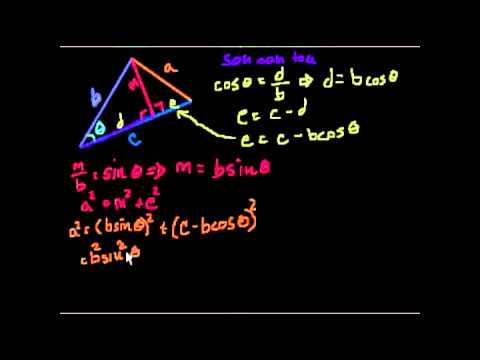
Зміст
Пошук вимірювання третьої сторони трикутника, коли ви знаєте вимірювання двох інших сторін, працює лише в тому випадку, якщо у вас є правильний трикутник або вимірювання принаймні одного іншого кута. Без цієї інформації у вас недостатньо даних для того, щоб дізнатися довжину третьої сторони. Правий трикутник має вбудований третій кут, оскільки один з кутів повинен бути 90 градусів.
Правий трикутник за допомогою теореми Піфагора
Намалюйте трикутник на папері, позначаючи дві сторони, що прилягають до прямого кута, або ніжки, "a" та "b". Намітьте гіпотенузу або третю сторону "c".
Складіть своє рівняння так, щоб: a2 + b2 = c2. Це теорема Піфагора, яка використовується для розв'язання невідомої сторони.
Заповніть відомі у рівнянні довжини. Гіпотенуза - це завжди найдовша сторона у правильному трикутнику. Це чудовий спосіб перевірити свою роботу, адже якщо одна з ніг довша гіпотенузи, ви знаєте, що ви допустили помилку.
Вирішіть для невідомої сторони. Якщо ви вирішуєте питання про гіпотенузу, ви заповнюєте квадрат "а" та "б", обидва числа і потім додаєте числа разом. Використовуйте калькулятор, щоб отримати квадратний корінь отриманої суми, щоб досягти своєї відповіді. Якщо ви вирішуєте одну з ніг, вам потрібно перемістити іншу ногу в ту ж сторону, що і «с», віднімаючи. Це залишає решту ноги в спокої, що дозволяє вирішити її. Це означає, що ви накреслили число "c" і відому ногу. Віднімаємо значення квадратної ніжки від значення c у квадраті. Отримайте квадратний корінь отриманого числа і у вас є відповідь на невідому ногу.
Використання закону про синуси
Встановіть трикутник так, щоб сторона, протилежна куту, відповідала куту. Позначте бічний протилежний кут A як a, сторону навпроти кута B як b, а сторону, протилежну куту C, як c.
Випишіть рівняння, щоб прочитати a / sinA = b / sinB = c / sinC. Це дає основи для вирішення для невідомої вам сторони.
Візьміть відомий вам кут і використовуйте калькулятор, щоб визначити синус цього кута. У більшості наукових калькуляторів ви вводите номер кута, а потім натискаєте кнопку з написом «гріх». Запишіть значення.
Розділіть довжину сторони, пов'язану з кутом, на значення гріха цього кута. Це дає вам число, яке, як правило, записується як наближення, оскільки десяткові знаки відпадають нескінченно. Назвіть це нове число X для цього прикладу.
Візьміть значення іншої відомої сторони і розділіть її на X. Це нове число дорівнює синусу нового кута.
Введіть число в калькулятор і натисніть «sin-1», щоб отримати кут у градусах. Тепер ви можете вирішити кут невідомої сторони.
Додайте два відомі кути разом і відніміть загальний від 180. Усі кути всередині трикутника повинні складати до 180 градусів.
Обчисліть синус нового кута, ввівши його в калькулятор і натиснувши кнопку «sin». Помножте відповідь на X, і це дає вам довжину невідомої сторони.
Для прикладу, що використовує теорему Піфагора, а також новий метод вирішення за допомогою Закону косинусів, дивіться відео нижче:
Порада: Закон Сінеса може бути викладений так, як заявлено, або перевернувши всю інформацію так, щоб синус кута ділився на довжину сторони.
Увага: Намалюйте проблему, щоб побачити, що ви множите і ділите, щоб зрозуміти, як працює проблема. Пам’ятайте, ви повинні зробити те саме, що обидві сторони рівняння, щоб сторони були рівними.